El Mayor Problema de Geometría
¿Cómo resolver un problema que se mantuvo abierto durante un siglo? En 1907, el famoso creador de puzles Henry Dudeney publicó un acertijo que se convirtió en una odisea para los matemáticos del siglo XX. Hubo que esperar cien años, hasta 2007, para que un estudiante del MIT consiguiera resolverlo. ¿Será “fácil” entender el mayor problema de geometría?
En este proyecto le darémos respuesta a este problema, dejando una reflexión tanto académica como personal. (Este es un proyecto para la Feria CIMAT 2020)
En la siguiente presentación hay un resumen de la respuesta a este problema:
Si quieres ver la presentación original puedes verla aquí, pero tendras que instalar las fuentes tipográficas que utilicé.
Historia y problema

En 1903, el famoso creador de puzles Henry Dudeney encontró una manera de cortar un triángulo en cuatro piezas que al reordenarlos podían formar un cuadrado. Lo interesante vino al descubrir que, si se colocaban bisagras en todas las piezas, la transformación seguía siendo válida, lo que resultó ser un deleite a la vista. Había nacido una pequeña rama de la geometría, más visual que provechosa: las Disecciones de Dudeney.
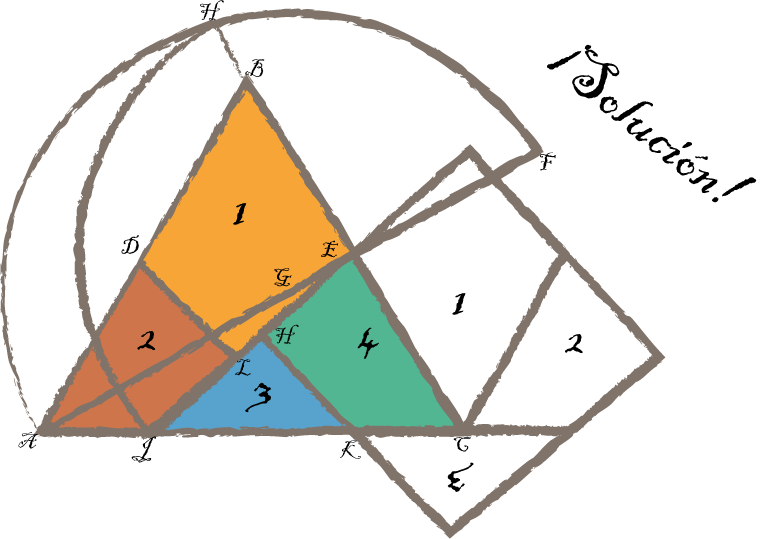
Con el tiempo, el mundo se llenó de disecciones de Dudeney entre distintas figuras: cuadrados, cruces, estrellas, triángulos, pentágonos y un sinfín más. Todas ellas, con piezas unidas con bisagras. Hasta que surgió la pregunta: “¿Cualquier pareja de figuras se puede transformar con piezas unidas por bisagras?”Con el tiempo, el mundo se llenó de disecciones de Dudeney entre distintas figuras: cuadrados, cruces, estrellas, triángulos, pentágonos y un sinfín más. Todas ellas, con piezas unidas con bisagras. Hasta que surgió la pregunta: “¿Cualquier pareja de figuras se puede transformar con piezas unidas por bisagras?”

Esta pregunta permaneció sin ser contestada durante más de un siglo; sin embargo, en 2007, un grupo de matemáticos del MIT propuso un método para convertir cualquier pareja de polígonos de la misma área con piezas encadenados entre sí.
Aparte de este método surgieron muchos otros que merecen ser conocidos como el método de las tiras.
Método de las Tiras
Este método permite construir disecciones de Dudeney con figuras no tan complicadas, por ejemplo, un triángulo y un cuadrado.
El primer paso consiste en transformar las dos figuras en tiras infinitas con la misma superficie, en el caso de el triángulo y el cuadrado es muy sencillo:
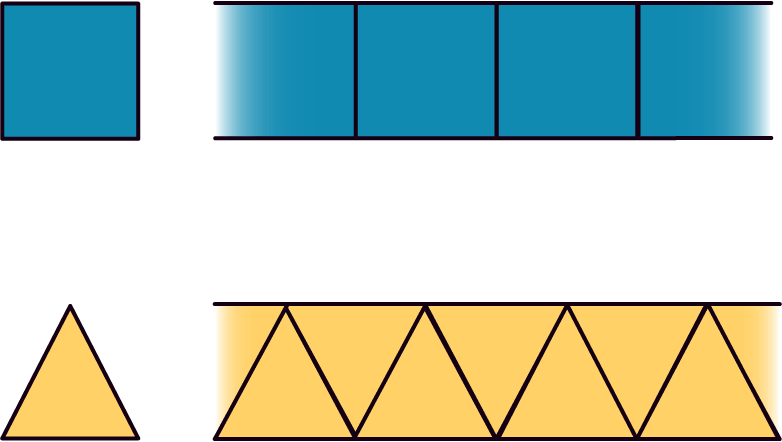
El segundo paso es observar la simetría de las tiras y buscar los puntos de anclaje. Los puntos de anclaje son puntos específicos donde puedes girar toda la tira 180 grados y quedarte en la misma situación. Son puntos con simetría de 180°:
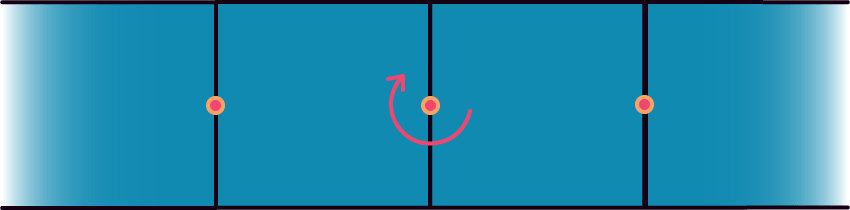
Los puntos de anclaje solo pueden situarse sobre las juntas entre las figuras que conforman la tira. No pueden estar dentro de la figura, sino solo sobre sus aristas

Para el tercer y último paso, tenemos que superponer las tiras de manera que en la intersección entre ambas los puntos de anclaje de una tira coincidan con los de la otra y también que coincidan los bordes de la otra tira. Si todo sigues bien los pasos y no quedan puntos de anclaje sueltos, tendrás como resultado una disección de Dudeney; las intersecciones resultantes te dirán cómo hacer los cortes e incluso dónde poner las bisagras.
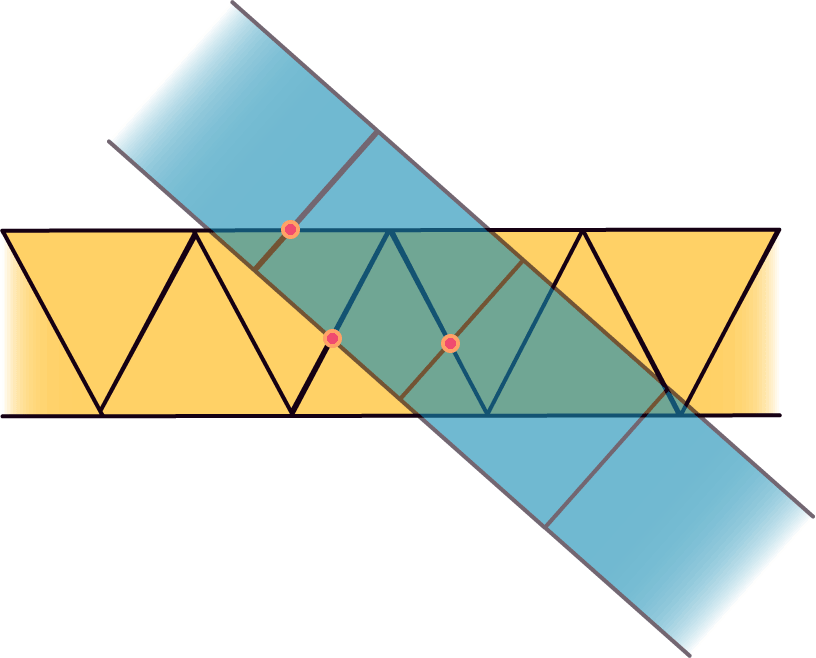
El resultado final de este método se vería así:
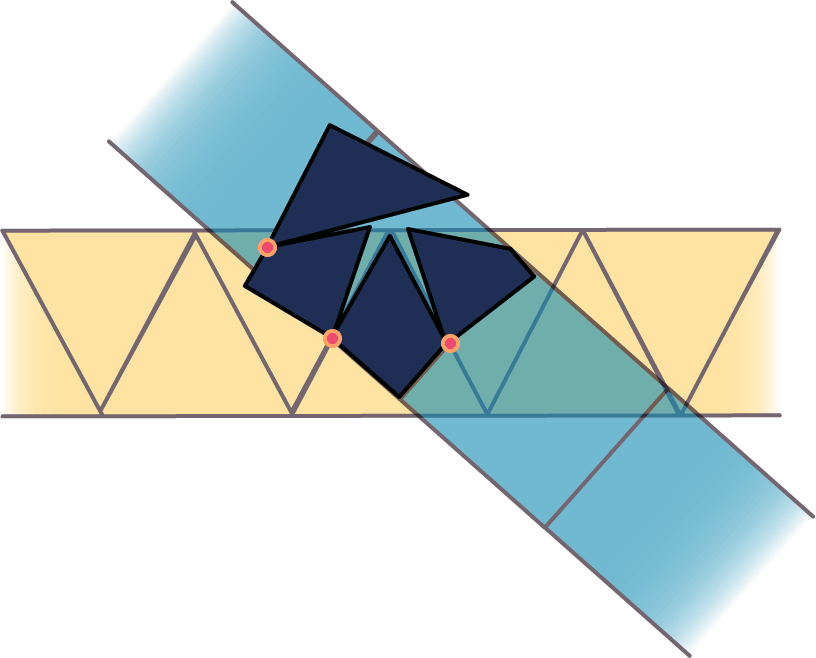
Sin embargo, este método se queda corto al intentarlo con figuras más complejas. Antes de contestar la pregunta inicial de este problema tenemos que entender las bases de su respuesta. Este es un consejo, si te enfrentas a un problema difícil, desármalo. Divídelo en partes que puedas controlar. Y es exactamente lo que haremos para responder este problema que duró más de un siglo.

Triángulo a Rectángulo
En este nivel reduciremos el nivel de dificultad de la pregunta inicial. Solamente le daremos respuesta a la siguiente pregunta: ¿Se puede transformar cualquier un triángulo en un rectángulo?
Sí, es posible y no es difícil, lo único que tienes que hacer es seguir una serie de pasos. Tan sencillos que incluso puedes a ver en tú casa, solo necesitas papel, tijera y guiarte por unas reglas.

Lo primero que tienes que hacer es apoyar el triángulo sobre la hipotenusa:
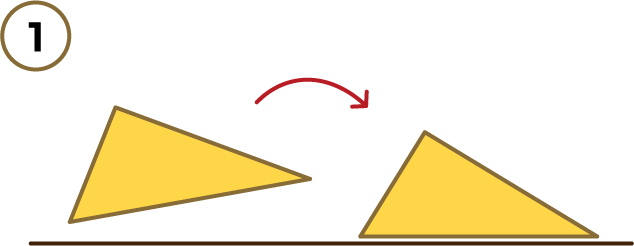
Dibujas la altura y haces un corte por la mitad:
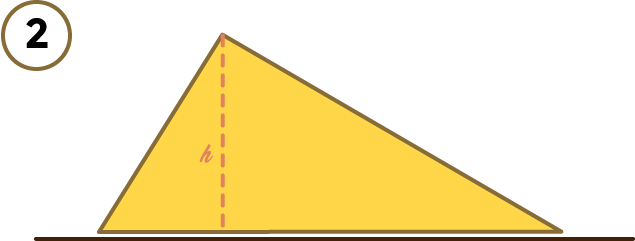
Haces un corte por la línea de la altura:
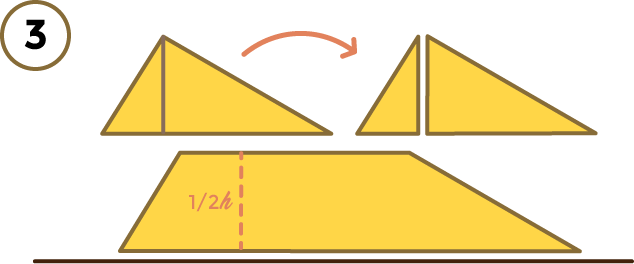
Por último, los trozos que has recortado encajan en la parte de abajo:
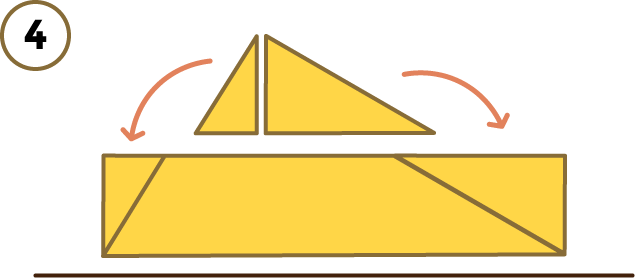
Y ya está, hemos transformado un triángulo en un rectángulo haciendo cortes. Este método funciona con cualquier triángulo inicial.
Pero tenemos un problema si el rectángulo final es más grueso o delgado; sin embargo, se puede resolver transformando los rectángulos de las siguientes formas:

La primera (Mitades) consiste en cortar el rectángulo por la mitad y tener suerte para que encaje con la forma que quieres obtener, pero si el rectángulo no encaja, entonces usamos el segundo método (Ajustar). Colocamos la forma del rectángulo final sobre el inicial, dibujamos la diagonal, cortamos y desplazamos. El pico que sobra al lado encaja en el hueco de arriba.

Dos figuras en general
En este nivel aumentáremos un poco más la dificulta de la pregunta: “¿Se puede transformar cualquier pareja de polígonos con piezas?”
La respuesta es que sí y si entendiste el nivel anterior este te resultará muy fácil.
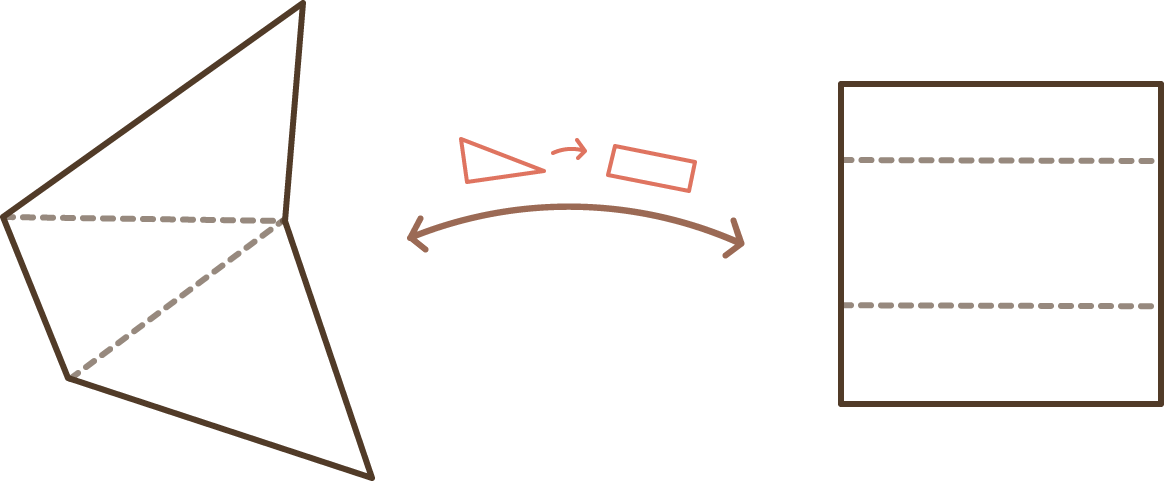
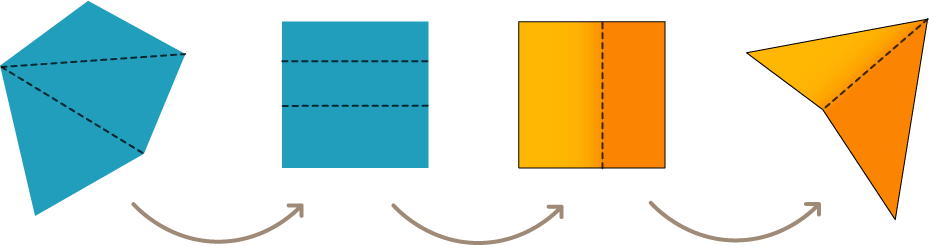
Dado que sin importar lo complicado que sea un polígono, puedes cortarlo en triángulos y los triángulos transformarlos en rectángulos. Y con unos ajustes puedes unir los rectángulos para crear un gran cuadrado. Este proceso también se puede hacer al viceversa, es decir convertir un cuadrado en cualquier figura final.
Y si unes los dos pasos puedes transformar cualquier pareja de figuras haciendo un pequeño intermedio en un cuadrado.
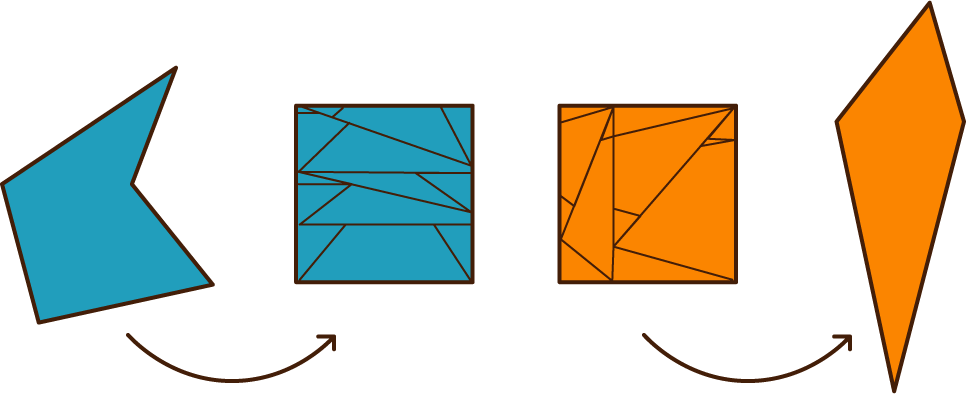
Esto es posible gracias a este teorema:
El teorema de Wallace-Bolyai-Gerwien
“Cualquier pareja de polígonos simples con la misma área se puede diseccionar en un número finito de piezas poligonales congruentes”

Disecciones de Dudeney
Ahora sí, le daremos respuesta al problema geométrico que estuvo abierto por más de un siglo.
“¿Cualquier pareja de figuras se puede transformar con piezas unidas por bisagras?”
Finalmente, la respuesta es que sí, siempre puedes. Esta respuesta consiste en usar los pasos anteriores y añadir bisagras donde puedas. Suena simple, ¿no?

En este caso utilizamos algo que se conoce como el método de la cadena que fue publicado en el artículo de 2007.
Método de la Cadena
Este método consiste en que para mover una pieza con bisagras tenemos que recortar dos cadenas, A y B. La principal que une la posición inicial y final, y una cadena gemela en el punto de llegada, las dos formadas por triángulos.

Por ejemplo, transformemos un triángulo en un cuadrado usando este método:

El primer paso es fácil porque le puedes colocar unas bisagras en las esquinas y todo sigue funcionando igual.

Por desgracia para el segundo paso tenemos que desplazar una pieza completa y no es posible añadir bisagras:

Es aquí donde hacemos uso del Método de la Cadena, para mover una pieza con bisagras hay que recortar dos cadenas una cadena principal que una la posición inicial y final, y una cadena gemela en el punto de llegada, las dos formas por triángulos.
En el caso de este cuadrado, las cadenas quedarían de esta manera:
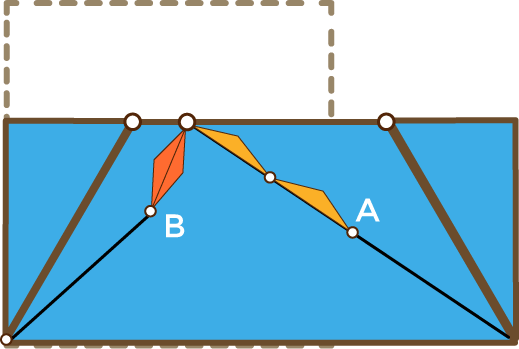
La principal que une la posición inicial al final y la gemela en el punto de llegada. Y para mover la pieza solo tienes que hacer lo siguiente:
Separaras la principal y separas la gemela:
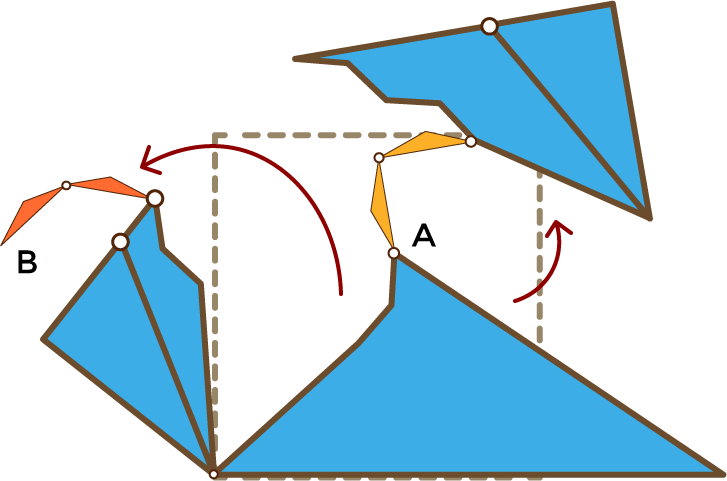
Guardas la principal, guardas la gemela y ya está:
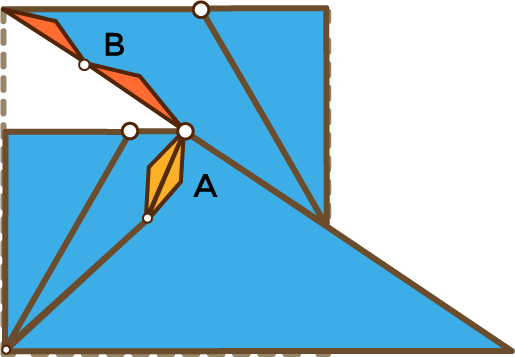
Para mover el último trozo a su posición final tenemos que construir una cadena bastante larga, buscamos un borde sobre el que recortarla y la recortamos. La cadena gemela también ocupa mucho espacio y tiene que estar muy plegada:
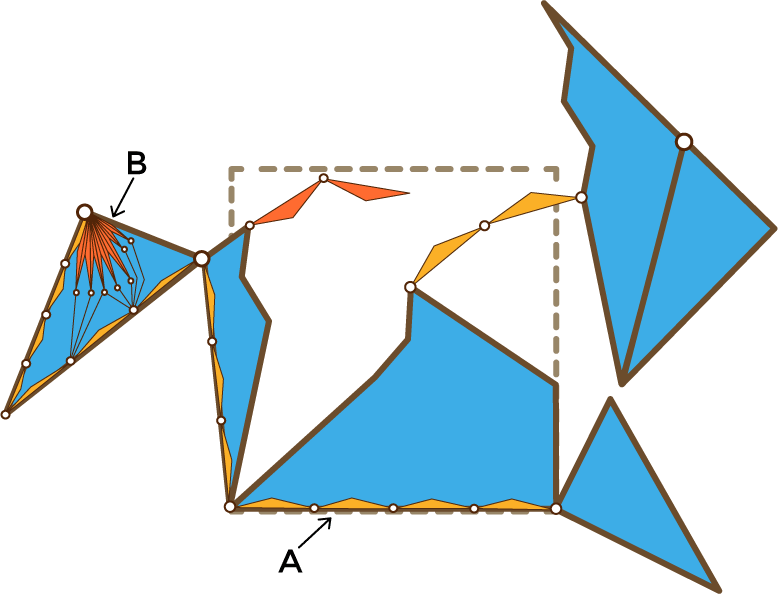
Aunque el aspecto sea muy complicado el método es el mismo. Desplegamos la cadena original y desplegamos la gemela:
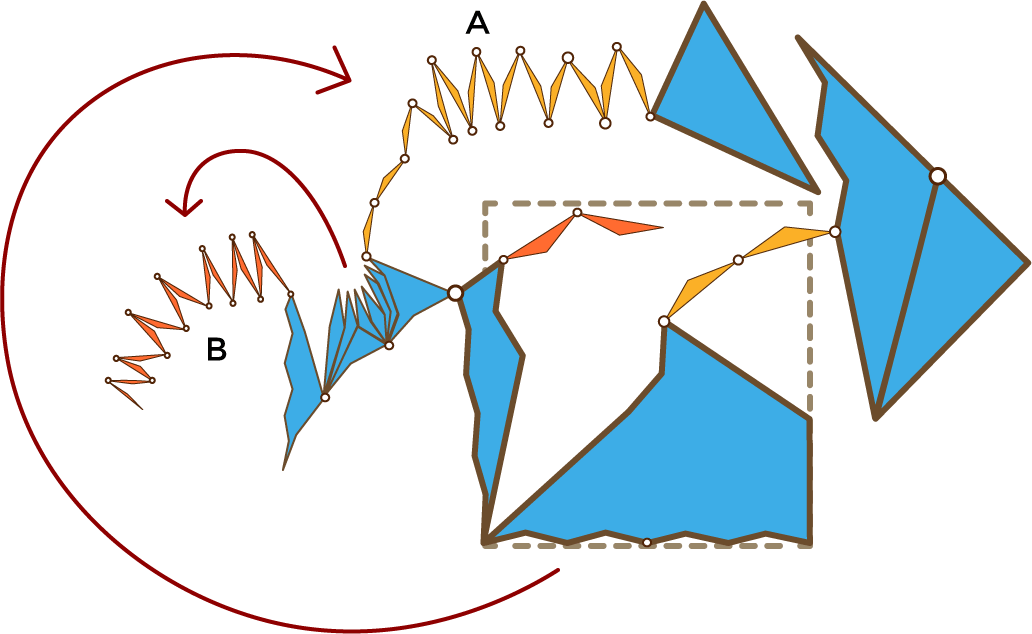
Guardamos la cadena original y guardamos la cadena gemela:
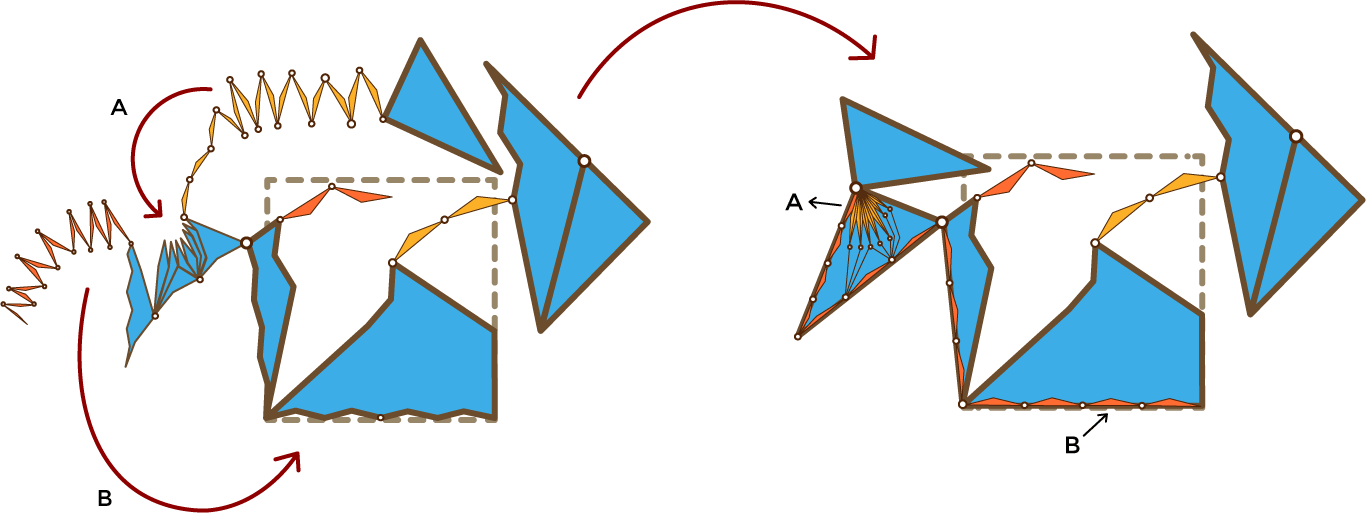
Por último, añadimos un par de cortes para plegar todo sin que se atraviesan las piezas y ya está:
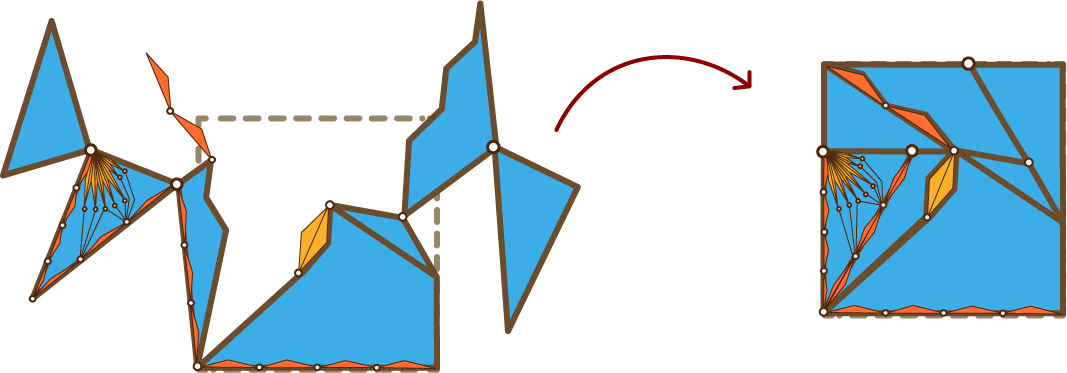
Hemos convertido un triángulo en un cuadrado con piezas encadenadas. Aunque sean muchos cortes y un poco complicado, este método sirve para cualquier figura inicial y final.
Conclusión
Gracias a los métodos de los niveles anteriores logramos darle respuesta al mayor problema de Geometría. El nivel 2 nos mostró qué forma tendrían las piezas y el nivel 3 cómo moverlas con bisagras y cadenas. Esto se puede aplicar a cualquier polígono.
En fin, este fue el problema geométrico que estuvo por más de un siglo sin resolver.
Y esto no solamente es interesante visualmente, si no que tiene algunas aplicaciones en la nano ingeniería y la robótica.
Este problema nos da una enseñanza básica tanto en matemáticas para resolver un problema complejo como para resolver problemas de vida real, siempre hay que empezar por resolver un problema más simple y elegir un buen punto de inicio.
